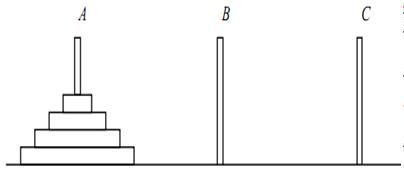
16. Методы разработки алгоритмов. Метод декомпозиции.

К настоящему времени специалисты по вычислительной технике разработали ряд эффективных методов, которые нередко позволяют получать эффективные алгоритмы решения больших классов задач. Некоторые из наиболее важных методов, такие как "разделяй и властвуй" (декомпозиции), динамическое программирование, "жадные" методы, поиск с возвратом и локальный поиск, представлены в этой главе. Пытаясь разработать алгоритм решения той или иной задачи, часто бывает полезно задать вопрос: "Какой тип решения позволяет получить метод декомпозиции, динамическое программирование, "жадный" метод или какой-либо другой стандартный метод?"

Возможно, самым важным и наиболее широко применимым методом проектирования эффективных алгоритмов является метод, называемый методом декомпозиции (или метод "разделяй и властвуй", или метод разбиения). Этот метод предполагает такую декомпозицию (разбиение) задачи размера n на более мелкие задачи, что на основе решений этих более мелких задач можно легко получить решение исходной задачи. Мы уже знакомы с рядом применений этого метода, например в сортировке слиянием или в деревьях двоичного поиска. Чтобы проиллюстрировать этот метод, рассмотрим хорошо известную головоломку "Ханойские башни". Имеются три стержня А, В и С. Вначале на стержень А нанизаны несколько дисков: диск наибольшего диаметра находится внизу, а выше — диски последовательно уменьшающегося диаметра, как показано на рис.. Цель головоломки — перемещать диски (по одному) со стержня на стержень так, чтобы диск большего диаметра никогда не размещался выше диска меньшего диаметра и чтобы в конце концов все диски оказались нанизанными на стержень В. Стержень С можно использовать для временного хранения дисков.

Для решения этой головоломки подходит следующий простой алгоритм. Представьте, что стержни являются вершинами треугольника. Пронумеруем все перемещения дисков. Тогда при перемещениях с нечетными номерами наименьший диск нужно перемещать в треугольнике на соседний стержень по часовой стрелке. При перемещениях с четными номерами выполняются другие допустимые перемещения, не связанные с наименьшим диском.

 
Задачу перемещения n наименьших дисков со стержня A на стержень B можно
 представить себе состоящей из двух подзадач размера n – 1.Сначала нужно
 переместить n – 1 наименьших дисков со стержня A на стержень C, оставив на
стержне A n-й наибольший диск. Затем этот диск нужно переместить с A на B.
 Потом следует переместить n – 1 дисков со стержня C на стержень B. Это
 перемещение n – 1 дисков выполняется путем рекурсивного применения указанного 
метода. Поменьше тех, которые в перемещении не участвуют, не нужно
задумываться над тем, что находится под перемещаемыми дисками на стержнях A,
 B или C.
  Хотя фактическое перемещение отдельных дисков не столь очевидно, а
моделирование вручную выполнить непросто из-за образования стеков рекурсивных
вызовов, с концептуальной точки зрения этот алгоритм все же довольно прост
для понимания и доказательства его правильности (а если говорить о быстроте
разработки, то ему вообще нет равных). Именно легкость разработки алгоритмов
по методу декомпозиции обусловила огромную популярность этого метода; к тому
же во многих случаях эти алгоритмы оказываются более эффективными, чем
алгоритмы, разработанные традиционными методами.
 

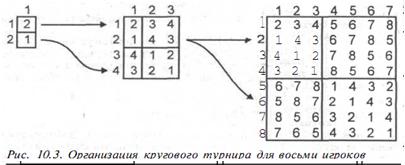
Расписание проведения турнира, таким образом, представляет собой таблицу, состоящую из л строк и п — 1 столбцов; элементом на пересечении строки i и столбца j является номер игрока, с которым игрок i должен провести матч в у'-й день. Метод декомпозиции позволяет составить расписание для половины игроков. Это расписание составляется на основе рекурсивного применения данного алгоритма для половины этой половины игроков и т.д. Когда количество игроков будет сокращено до двух, возникнет "базовая ситуация", в которой мы просто устанавливаем порядок проведения встреч между ними. Допустим, в турнире участвуют восемь игроков. Расписание для игроков 1 - 4 заполняет верхний левый угол (4 строки х З столбца) составляемого расписания. Нижний левый угол (4 строки х З столбца) этого расписания должен свести между собой игроков с более высокими номерами (5 - 8). Эта часть расписания получается путем прибавления числа 4 к каждому элементу в верхнем левом углу.

Итак, нам удалось упростить задачу. Теперь остается свести между собой игроков с низкими и более высокими номерами. Сделать это нетрудно: надо на 4-й день свести в пары игроков, имеющих номера 1 - 4, с игроками 5-8 соответственно, а в последующие дни просто циклически переставлять номера 5 - 8. Этот процесс показан на рис. 10.3. Надеемся, теперь читатель сможет обобщить описанный алгоритм и составить расписание для 2* игроков при любом значении k.